РАСЧЕТ АЭРОДИНАМИЧЕСКИХ ХАРАКТЕРИСТИК ВОЗДУШНЫХ ВИНТОВ ЧИСЛЕННЫМИ МЕТОДАМИВ шестом номере "АОН" за 1999 г. авторы рассмотрели задачу аэродинамического проектирования оптимального воздушного винта фиксированного шага, обеспечивающего максимум тяги при минимальных индуктивных и профильных потерях винта на заданном режиме полета. В статье был рассмотрен пример применения предложенного метода для определения геометрии лопасти винта, оптимизированного на крейсерскую скорость V=150 км/ч, к самолету с двигателем ROTAX-582. Параметры винта, выбранные оптимальными для крейсерского режима полета самолета, как правило, далеки от оптимальных на взлете. Так, на режиме взлета винт может оказаться сильно перегруженным и не реализовать требуемую величину тяги для обеспечения заданных взлетно-посадочных характеристик самолета. В связи с этим после проектировочного расчета винта [1] необходимо выполнить проверочные расчеты во всем эксплуатационном диапазоне скоростей полета. В результате этих расчетов определяются суммарные и распределенные аэродинамические характеристики винта, высотно-скоростные характеристики силовой установки самолета, исследуется возмущенное поле скоростей в окрестности винта. В настоящее время для проведения расчетов воздушных винтов с заданной геометрией лопасти широко применяются на практике два хорошо зарекомендовавших себя численных метода:
Применение этих методов позволяет использовать положительные стороны и преимущества каждого из них при решении конкретной прикладной задачи. Например, вихревая теория винта позволяет оперативно выполнять параметрические исследования, а метод дискретных вихрей - определять поле течения в его окрестности, уточнять распределенные и суммарные характеристики, исследовать интерференционные эффекты. Рассмотрим кратко основные положения этих численных методов. НЕЛИНЕЙНАЯ ВИХРЕВАЯ ТЕОРИЯ ВИНТА С КОНЕЧНЫМ ЧИСЛОМ ЛОПАСТЕЙЧисленный метод расчета разработан на основе работ Г.И.Майкопара и А.М.Лепелкина по вихревой теории винта [2-4]. Основные положения и допущения этой теории следующие:
Вследствие второго допущения пренебрегаем влиянием пространственности течения, то есть не учитываем образование концевых вихрей и околовтулочные течения, а также радиальные течения под действием центробежных сил. При построении расчетной схемы винта используется подход, изложенный в работе [2]. Несущая поверхность лопасти заменяется присоединенным радиальным вихрем с переменной по длине циркуляцией. Сходящая с лопастей вихревая пелена моделируется системой вихрей, состоящей из полубесконечных винтообразных свободных вихрей постоянного в осевом направлении диаметра и шага. Шаг свободных вихрей рассчитывается не по скорости невозмущенного потока, а с учетом индуктивных скоростей от всей вихревой системы винта. Рассмотрим обтекание профиля лопасти винта в произвольном сечении плоскопараллельным потоком (рис. 1). Из приведенного треугольника скоростей находим местный угол атаки профиля лопасти: (1)
Из условия равенства нулю радиальной составляющей индуктивной скорости можно записать: (2)
Применяя к свободным вихрям формулу Био-Савара, получим выражения для тангенциальной составляющей индуктивной скорости: (3) (4)
Полученный интеграл (4) имеет особенности, и в работах [2,4] предложены различные способы вычисления данного интеграла. В настоящей работе рассмотрен подход, основанный на замене истинного распределения циркуляции по радиусу лопасти эллиптическим. С учетом этого, выражение для тангенциальной составляющей индуктивной скорости (3) преобразуется к виду: (5)
На основе данного подхода с помощью формул (1) - (2) определяется угол атаки сечения лопасти и, используя аэродинамические характеристики заданных профилей, циркуляция в рассматриваемом сечении. Вычисление циркуляции в каждом сечении осуществляется методом последовательных приближений. Зная циркуляцию и кинематические характеристики лопасти в расчетных сечениях, находим аэродинамические характеристики винта в целом: (6)
Рассмотренная нелинейная вихревая теория винта базируется на гипотезе плоских сечений и дает хорошие результаты при условии безотрывного обтекания всех расчетных сечений лопасти. На некоторых режимах работы винта в прикомлевых сечениях лопасти истинные углы атаки сечений превышают критические. Возникающий срыв потока в этих сечениях представляет более сложное явление, чем срыв на профиле крыла. Это обусловлено нестационарностью и пространственностью обтекания прикомлевых сечений. При нестационарном (динамическом) срыве сечения лопасти способны создавать большую подъемную силу, чем при срыве на профиле крыла, при этом значительно возрастает сопротивление и коэффициент профильных потерь мощности. В работах [5,6] рассмотрены основные закономерности развития динамического срыва с профиля лопасти и методы его расчета. На основе этих методов авторами был предложен подход, позволяющий рассчитывать в рамках вихревой теории аэродинамические характеристики винта при наличии динамического срыва с тех участков лопастей, где местные углы атаки сечений превышают критические. На основе нелинейной вихревой теории винта с конечным числом лопастей была разработана программа расчета аэродинамических характеристик винта при заданной геометрии лопасти с учетом динамического срыва потока. На рис.2 представлены расчетные зависимости коэффициента мощности двухлопастного винта от относительной поступи при двух значениях угла установки =200 и 250. Здесь же приведены экспериментальные данные работы [7]. Из приведенных графиков следует, что при больших углах атаки установки лопасти >200 расчет с учетом динамического срыва обеспечивает удовлетворительное совпадение расчетных и экспериментальных данных при нулевых и околонулевых скоростях полета (). НЕЛИНЕЙНАЯ НЕСТАЦИОНАРНАЯ ТЕОРИЯ ВИНТАВ представленной статье нелинейная нестационарная теория винта [8,9] применена к задачам исследования аэродинамики самолетного воздушного винта и его интерференции с другими частями летательного аппарата (кольцо, горизонтальное и вертикальное оперение и т.д.), где использование вихревой теории винта, базирующейся на методах плоских сечений, является малоэффективной. При решении этой задачи используются общепринятые в нелинейной теории винта [8,9] гипотезы и допущения:
Для численного решения задачи несущие поверхности лопастей винта и вихревой след за ними моделируются замкнутыми вихревыми рамками. Это позволило использовать модульный принцип построения расчетной вихревой схемы, что оказалось весьма эффективным при решении интерференционных задач. Расчетная вихревая схема одной лопасти винта представлена на рис. 3.
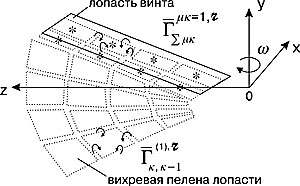
Выполняя граничное условие непротекания лопасти в каждой расчетной точке, получим систему линейных алгебраических уравнений для определения напряженностей присоединенных вихревых рамок (7) (8)
По найденным значениям напряженностей вихревых рамок , моделирующих лопасть винта, определяем безразмерную аэродинамическую нагрузку в расчетных точках (9) (10) Величина определяется численным дифференцированием циркуляций вихревых рамок. Интегрируя распределенную аэродинамическую нагрузку по несущим поверхностям лопастей находим интегральные аэродинамические характеристики винта (11) (12) Найденные из решения системы (7) напряженности вихревых рамок позволяют рассчитать поле скоростей в окрестности винта и выстроить положение вихревой пелены. Таким образом, в процессе расчета получаем полную информацию о вихревой структуре винта и возмущенном поле скоростей. Задача решается методом установления дискретными шагами по времени. Разработанная на основе данной теории программа расчета позволяет рассчитывать не только аэродинамические характеристики изолированного винта, но и исследовать его взаимодействие с другими элементами планера самолета, чему будут посвящены следующие статьи авторов. ПРАКТИЧЕСКОЕ ПРИМЕНЕНИЕ ЧИСЛЕННЫХ МЕТОДОВВ статье [1] авторы рассмотрели задачу аэродинамического проектирования воздушного винта фиксированного шага к легкому самолету с двигателем ROTAX-582, который имеет редуктор с передаточным числом i = 2,0. Трехлопастной винт диаметром D = 1,35 м был оптимизирован на крейсерскую скорость полета V = 150 км/ч. Геометрические параметры лопасти данного винта и ее профилировка представлены на рис.1,4,5 работы [1]. Из представленных расчетных данных следует, что спроектированный винт при использовании располагаемой мощности двигателя ROTAX-582 (n = 6000 об/мин) обеспечивает коэффициент тяги =0,092, что соответствует значению тяги винта P = 95 кг при полете у земли на скорости V=150 км/ч. С практической точки зрения большой интерес представляют аэродинамические характеристики спроектированного винта . Относительная поступь винта на взлетном режиме равна нулю, при полете на скорости V=150 км/ч и частоте вращения винта n = 3000 об/мин = 0,61. На основе нелинейной вихревой теории винта были рассчитаны зависимости коэффициентов тяги, мощности и к.п.д от относительной поступи спроектированного винта (рис.4) для принятой геометрии и крутки лопасти. При скорости V = 150 км/ч ( = 0,61) расчетные значения коэффициентов тяги и мощности соответственно равны 0,092 и 0,07, что соответствует параметрам спроектированного винта. Винт фиксированного шага, оптимизированный на скорость V=150 км/ч, может оказаться перегруженным на взлетном режиме, что приводит к снижению угловой скорости вращения винта и падению его тяги. В связи с этим важной задачей является расчет высотно-скоростных характеристик силовой установки летательного аппарата (комбинация винт и двигатель), которые являются основой для определения летно-технических характеристик самолета. Расчет высотно-скоростных характеристик спроектированного трехлопастного винта с двигателем ROTAX-582 осуществлялся на основе совместного анализа кривых располагаемого крутящего момента на валу двигателя Mp(n) и потребного крутящего момента на оси винта Mв(n) для определенного режима полета. Зависимость располагаемого крутящего момента двигателя от частоты вращения коленчатого вала Mp(n) обычно приводится в его паспортных данных [10] или рассчитывается на основе его внешней характеристики. Располагаемая мощность двигателя для различных высот рассчитывается на основе соотношений (13) (14)
На рис.5 сплошными линиями показаны зависимости располагаемого крутящего момента двигателя ROTAX-582 на валу винта Мр(n) для высоты H=0 и двух режимов: взлетного (Np) и номинального (0,75Np). Здесь же нанесены зависимости потребного крутящего момента винта Мв(n) для различных скоростей полета при H=0. Зависимости Мв(n,V) рассчитываются на основе зависимости , представленной на рис.4. Точки пересечения кривых располагаемого крутящего момента двигателя Мp(n) и потребного момента винта Мв(n) соответствуют частоте установившегося вращения винта на заданном режиме. С учетом зависимости (рис. 4) строится зависимость тяги винта от частоты вращения вала P(n) (рис.6) для различных скоростей полета. Нанося на кривые P(n) значения установившейся частоты вращения винта, получим величину тяги винта для заданной скорости. Используя данные рис.6, можно построить скоростные характеристики двигателя с заданным винтом на H = 0 м для двух режимов его работы. Нанося на данный график зависимость лобового сопротивления самолета в горизонтальном полете от скорости Xa(V) (штрих-пунктирная линия на рис.6), определяем максимальные скорости горизонтального полета Vmax для каждого режима работы двигателя. При выполнении прочностных расчетов проектируемого винта необходимо знать распределение аэродинамической нагрузки по хорде и радиусу лопасти винта. Нелинейная нестационарная теория винта дает возможность рассчитать распределенные аэродинамические характеристики винта и определить возмущенное поле скоростей в его окрестности.
В качестве примера на рис.7 представлены зависимости коэффициента подъемной силы сечений лопасти вдоль радиуса винта для двух режимов его работы. На взлетном режиме (V = 0, nв = 2000 об/мин) в прикомлевых сечениях лопасти значения коэффициента подъемной силы Су`а превышают стационарные значения Cy`max соответствующих винтовых профилей, то есть данные участки лопасти работают в условиях динамического срыва потока. На скорости V = 150 км/ч распределение Су`а(r) соответствует оптимальному винту и не превышает максимальные значения Cy`max. Рис.8 иллюстрирует распределение безразмерной аэродинамической нагрузки вдоль хорды лопасти для различных сечений на взлетном режиме, а рис.9 - векторное поле возмущенных скоростей за изолированным винтом для скорости V = 100 км/ч.
Изложенные в настоящей статье численные методы расчета аэродинамических характеристик изолированных воздушных винтов и разработанные на их основе рабочие программы используются в АО "Научно-промышленный сервис" при разработке легкого самолета "Феникс 2" и ДПЛА "Ремез-3". Е.Д.Ковалев, В.А.Удовенко Литература
|